How To Calculate Crystal Field Splitting Energy

A outcome of Crystal Field Theory is that the distribution of electrons in the d orbitals may lead to cyberspace stabilization (subtract in energy) of some complexes depending on the specific ligand field geometry and metal d-electron configurations. It is a simple matter to calculate this stabilization since all that is needed is the electron configuration and knowledge of the splitting patterns.

Definition: Crystal Field Stabilization Energy

The Crystal Field Stabilization Energy is divers as the energy of the electron configuration in the ligand field minus the energy of the electronic configuration in the isotropic field.

\[CFSE=\Delta{East}=E_{\text{ligand field}} - E_{\text{isotropic field}} \label{ane}\]

The CSFE volition depend on multiple factors including:

• Geometry (which changes the d-orbital splitting patterns)
• Number of d-electrons
• Spin Pairing Energy
• Ligand character (via Spectrochemical Series)

For an octahedral complex, an electron in the more than stable \(t_{2g}\) subset is treated as contributing \(-2/v\Delta_o\) whereas an electron in the higher energy \(e_g\) subset contributes to a destabilization of \(+three/v\Delta_o\). The last answer is so expressed as a multiple of the crystal field splitting parameter \(\Delta_o\). If whatever electrons are paired within a single orbital, then the term \(P\) is used to correspond the spin pairing energy.

Instance \(\PageIndex{1}\): CFSE for a high Spin \(d^seven\) complex

What is the Crystal Field Stabilization Energy for a high spin \(d^7\) octahedral complex?

Solution

The splitting pattern and electron configuration for both isotropic and octahedral ligand fields are compared below.

The energy of the isotropic field \((E_{\text{isotropic field}}\)) is

\[ E_{\text{isotropic field}}= seven \times 0 + 2P = 2P \nonumber \]

The energy of the octahedral ligand field \(E_{\text{ligand field}}\) is

\[E_{\text{ligand field}} = (5 \times -2/5 \Delta_o ) + (2 \times 3/5 \Delta_o) + 2P = -4/5 \Delta_o + 2P \nonumber \]

So via Equation \ref{one}, the CFSE is

\[\begin{align} CFSE &=E_{\text{ligand field}} - E_{\text{isotropic field}} \nonumber \\[4pt] &=( -4/v\Delta_o + 2P ) - 2P \nonumber \\[4pt] &=-4/five \Delta_o \nonumber \stop{align} \nonumber \]

Discover that the Spin pairing Free energy falls out in this case (and volition when computing the CFSE of high spin complexes) since the number of paired electrons in the ligand field is the same equally that in isotropic field of the free metal ion.

Example \(\PageIndex{2}\): CFSE for a Low Spin \(d^vii\) circuitous

What is the Crystal Field Stabilization Energy for a depression spin \(d^7\) octahedral complex?

Solution

The splitting design and electron configuration for both isotropic and octahedral ligand fields are compared beneath.

The energy of the isotropic field is the same as calculated for the high spin configuration in Example 1:

\[ E_{\text{isotropic field}}= 7 \times 0 + 2P = 2P \nonumber\]

The energy of the octahedral ligand\) field \(E_{\text{ligand field}}\) is

\[\begin{marshal} E_{\text{ligand field}} &= (half-dozen \times -2/5 \Delta_o ) + (i \times three/5 \Delta_o) + 3P \nonumber \\[4pt] &= -9/5 \Delta_o + 3P \nonumber \cease{marshal} \nonumber \]

And so via Equation \ref{i}, the CFSE is

\[\begin{align} CFSE&=E_{\text{ligand field}} - E_{\text{isotropic field}} \nonumber \\[4pt] &=( -9/5 \Delta_o + 3P ) - 2P \nonumber \\[4pt] &=-9/5 \Delta_o + P \nonumber \end{align} \nonumber \]

Adding in the pairing energy since it will crave actress energy to pair up one extra grouping of electrons. This appears more a more stable configuration than the high spin \(d^7\) configuration in Example \(\PageIndex{1}\), but we have then to have into consideration the Pairing energy \(P\) to know definitely, which varies between \(200-400\; kJ\; mol^{-ane}\) depending on the metal.

Table \(\PageIndex{one}\): Crystal Field Stabilization Energies (CFSE) for high and low spin octahedral complexes

Full d-electrons	Isotropic Field	Octahedral Complex				Crystal Field Stabilization Free energy
		High Spin		Depression Spin
	\(E_{\text{isotropic field}}\)	Configuration	\(E_{\text{ligand field}}\)	Configuration	\(E_{\text{ligand field}}\)	Loftier Spin	Low Spin
d0	0	\(t_{2g}\)0\(e_g\)0	0	\(t_{2g}\)0\(e_g\)0	0	0	0
dane	0	\(t_{2g}\)1\(e_g\)0	-2/v \(\Delta_o\)	\(t_{2g}\)1\(e_g\)0	-2/5 \(\Delta_o\)	-ii/5 \(\Delta_o\)	-2/5 \(\Delta_o\)
dtwo	0	\(t_{2g}\)2\(e_g\)0	-4/5 \(\Delta_o\)	\(t_{2g}\)2\(e_g\)0	-four/5 \(\Delta_o\)	-4/5 \(\Delta_o\)	-4/v \(\Delta_o\)
dthree	0	\(t_{2g}\)iii\(e_g\)0	-6/5 \(\Delta_o\)	\(t_{2g}\)3\(e_g\)0	-6/5 \(\Delta_o\)	-six/5 \(\Delta_o\)	-6/5 \(\Delta_o\)
d4	0	\(t_{2g}\)3\(e_g\)1	-3/5 \(\Delta_o\)	\(t_{2g}\)iv\(e_g\)0	-8/5 \(\Delta_o\) + P	-3/five \(\Delta_o\)	-8/5 \(\Delta_o\) + P
d5	0	\(t_{2g}\)three\(e_g\)2	0 \(\Delta_o\)	\(t_{2g}\)v\(e_g\)0	-x/v \(\Delta_o\) + 2P	0 \(\Delta_o\)	-ten/five \(\Delta_o\) + 2P
d6	P	\(t_{2g}\)4\(e_g\)2	-two/5 \(\Delta_o\) + P	\(t_{2g}\)6\(e_g\)0	-12/5 \(\Delta_o\) + 3P	-two/5 \(\Delta_o\)	-12/five \(\Delta_o\) + P
d7	2P	\(t_{2g}\)v\(e_g\)2	-4/5 \(\Delta_o\) + 2P	\(t_{2g}\)half-dozen\(e_g\)ane	-9/5 \(\Delta_o\) + 3P	-4/5 \(\Delta_o\)	-9/v \(\Delta_o\) + P
dviii	3P	\(t_{2g}\)half dozen\(e_g\)2	-half-dozen/5 \(\Delta_o\) + 3P	\(t_{2g}\)half-dozen\(e_g\)2	-6/5 \(\Delta_o\) + 3P	-6/5 \(\Delta_o\)	-6/5 \(\Delta_o\)
dnine	4P	\(t_{2g}\)6\(e_g\)3	-3/5 \(\Delta_o\) + 4P	\(t_{2g}\)six\(e_g\)3	-3/5 \(\Delta_o\) + 4P	-3/five \(\Delta_o\)	-iii/v \(\Delta_o\)
dx	5P	\(t_{2g}\)6\(e_g\)4	0 \(\Delta_o\) + 5P	\(t_{2g}\)vi\(e_g\)4	0 \(\Delta_o\) + 5P	0	0

\(P\) is the spin pairing energy and represents the energy required to pair up electrons inside the same orbital. For a given metal ion P (pairing energy) is constant, only it does not vary with ligand and oxidation state of the metal ion).

Octahedral Preference

Like CFSE values can be constructed for non-octahedral ligand field geometries once the knowledge of the d-orbital splitting is known and the electron configuration inside those orbitals known, due east.g., the tetrahedral complexes in Table \(\PageIndex{ii}\). These energies geoemtries tin can then be contrasted to the octahedral CFSE to calculate a thermodynamic preference (Enthalpy-wise) for a metal-ligand combination to favor the octahedral geometry. This is quantified via a Octahedral Site Preference Energy defined below.

Definition: Octahedral Site Preference Energies

The Octahedral Site Preference Energy (OSPE) is defined as the departure of CFSE energies for a not-octahedral complex and the octahedral circuitous. For comparing the preference of forming an octahedral ligand field vs. a tetrahedral ligand field, the OSPE is thus:

\[OSPE = CFSE_{(oct)} - CFSE_{(tet)} \label{2}\]

The OSPE quantifies the preference of a complex to exhibit an octahedral geometry vs. a tetrahedral geometry.

Note: the conversion betwixt \(\Delta_o\) and \(\Delta_t\) used for these calculations is:

\[\Delta_t \approx \dfrac{4}{ix} \Delta_o \label{three}\]

which is applicable for comparing octahedral and tetrahedral complexes that involve same ligands only.

Table \(\PageIndex{2}\): Octahedral Site Preference Energies (OSPE)

Full d-electrons	CFSE(Octahedral)		CFSE(Tetrahedral)		OSPE (for high spin complexes)**
	High Spin	Depression Spin	Configuration	Always Loftier Spin*
d0	0 \(\Delta_o\)	0 \(\Delta_o\)	e0	0 \(\Delta_t\)	0 \(\Delta_o\)
done	-2/5 \(\Delta_o\)	-two/v \(\Delta_o\)	east1	-3/five \(\Delta_t\)	-6/45 \(\Delta_o\)
dtwo	-4/5 \(\Delta_o\)	-iv/five \(\Delta_o\)	easttwo	-half-dozen/5 \(\Delta_t\)	-12/45 \(\Delta_o\)
d3	-6/5 \(\Delta_o\)	-6/5 \(\Delta_o\)	due eastiit2 1	-iv/v \(\Delta_t\)	-38/45 \(\Delta_o\)
d4	-3/five \(\Delta_o\)	-8/5 \(\Delta_o\) + P	e2t2 ii	-2/five \(\Delta_t\)	-xix/45 \(\Delta_o\)
dfive	0 \(\Delta_o\)	-ten/v \(\Delta_o\) + 2P	e2t2 3	0 \(\Delta_t\)	0 \(\Delta_o\)
d6	-2/5 \(\Delta_o\)	-12/v \(\Delta_o\) + P	e3t2 three	-iii/5 \(\Delta_t\)	-half dozen/45 \(\Delta_o\)
d7	-iv/5 \(\Delta_o\)	-9/5 \(\Delta_o\) + P	e4t2 3	-6/five \(\Delta_t\)	-12/45 \(\Delta_o\)
d8	-6/v \(\Delta_o\)	-six/5 \(\Delta_o\)	e4ttwo 4	-four/v \(\Delta_t\)	-38/45 \(\Delta_o\)
d9	-three/5 \(\Delta_o\)	-3/five \(\Delta_o\)	e4tii 5	-2/5 \(\Delta_t\)	-19/45 \(\Delta_o\)
d10	0	0	e4t2 vi	0 \(\Delta_t\)	0 \(\Delta_o\)

\(P\) is the spin pairing energy and represents the energy required to pair up electrons within the aforementioned orbital.

Tetrahedral complexes are e'er high spin since the splitting is appreciably smaller than \(P\) (Equation \ref{3}).

Afterward conversion with Equation \ref{3}. The information in Tables \(\PageIndex{1}\) and \(\PageIndex{2}\) are represented graphically by the curves in Effigy \(\PageIndex{i}\) below for the high spin complexes only. The low spin complexes require noesis of \(P\) to graph.

Figure \(\PageIndex{1}\): Crystal Field Stabilization Energies for both octahedral fields (\(CFSE_{oct}\)) and tetrahedral fields (\(CFSE_{tet}\)). Octahedral Site Preference Energies (OSPE) are in yellow. This is for loftier spin complexes.

From a unproblematic inspection of Figure \(\PageIndex{1}\), the post-obit observations can exist fabricated:

• The OSPE is pocket-sized in \(d^1\), \(d^2\), \(d^v\), \(d^six\), \(d^7\) complexes and other factors influence the stability of the complexes including steric factors
• The OSPE is large in \(d^3\) and \(d^8\) complexes which strongly favor octahedral geometries

Applications

The "double-humped" curve in Figure \(\PageIndex{1}\) is found for various properties of the first-row transition metals, including Hydration and Lattice energies of the Thou(II) ions, ionic radii as well as the stability of M(II) complexes. This suggests that these backdrop are somehow related to Crystal Field effects.

In the case of Hydration Energies describing the complexation of water ligands to a bare metal ion:

\[1000^{2+} (yard) + H_2O \rightarrow [Thou(OH_2)_6]^{2+} (aq)\]

Table \(\PageIndex{3}\) and Effigy \(\PageIndex{i}\) shows this type of curve. Annotation that in any series of this type non all the information are available since a number of ions are not very stable in the M(Two) state.

Table \(\PageIndex{three}\): Hydration energies of \(M^{2+}\) ions

M	ΔH°/kJmol-ane	One thousand	ΔH°/kJmol-1
Ca	-2469	Fe	-2840
Sc	no stable 2+ ion	Co	-2910
Ti	-2729	Ni	-2993
>Five	-2777	Cu	-2996
Cr	-2792	Zn	-2928
Mn	-2733

Graphically the information in Table 2 can be represented past:

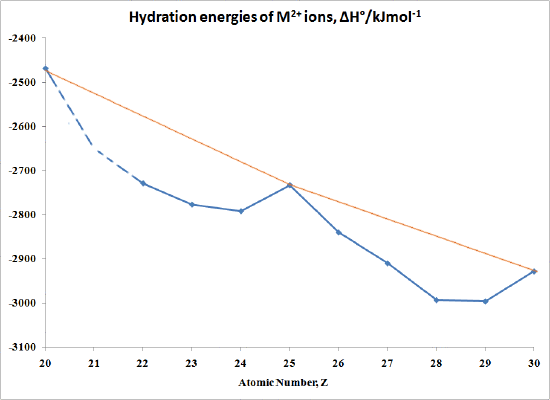
Figure \(\PageIndex{ii}\): hydration energies of \(K^{2+}\) ions

Source: https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_and_Websites_%28Inorganic_Chemistry%29/Crystal_Field_Theory/Crystal_Field_Stabilization_Energy

Share this post