25 99 As A Decimal
Wondering how to convert decimals to fractions? Or how to convert fractions to decimals? Information technology's easier than y'all think! Keep reading to see the steps for decimal to fraction conversions (including why you need to follow different steps if you have a repeating decimal), steps for fraction to decimal conversions, a handy chart with common decimal/fraction conversions, and tips for quickly estimating conversions. How do you convert a decimal to a fraction? Whatsoever decimal, even complicated-looking ones, can be converted to a fraction; y'all just need to follow a few steps. Below nosotros explain how to catechumen both terminating decimals and repeating decimals to fractions. A terminating decimal is whatsoever decimal that has a finite other of digits. In other words, information technology has an cease. Examples include .5, .234, .864721, etc. Terminating decimals are the most common decimals yous'll run across and, fortunately, they are also the easiest to convert to fractions. Write the decimal divided by one. For instance, say you're given the decimal .55.Your starting time step is to write out the decimal then it looks like ${.55}/{one}$. Side by side, you desire to multiply both the superlative and bottom of your new fraction past 10 for every digit to the left of the decimal signal. In our case, .55 has two digits later on the decimal point, and so we'll want to multiply the unabridged fraction by x x 10, or 100. Multiplying the fraction past ${100}/{100}$ gives us ${55}/{100}$. The final step is reducing the fraction to its simplest form. The simplest class of the fraction is when the summit and bottom of the fraction are the smallest whole numbers they tin can be. For case, the fraction ${iii}/{9}$ isn't in its simplest form because it can even so be reduced downwards to ⅓ by dividing both the top and bottom of the fraction past 3. The fraction ${55}/{100}$ tin can exist reduced by dividing both the top and bottom of the fraction by v, giving us ${11}/{20}$. 11 is a prime number and can't be divided any more than, and so we know this is the fraction in its simplest course. The decimal .55 is equal to the fraction ${11}/{20}$. Convert .108 to a fraction. After putting the decimal over 1, we end up with ${.108}/{one}$. Since .108 has three digits after the decimal place, nosotros need to multiply the unabridged fraction past 10 x 10 x x, or one thousand. This gives us ${108}/{grand}$. Now we need to simplify. Since 108 and thou are both even numbers, we know we tin separate both by 2. This gives u.s.a. ${54}/{500}$. These are still even numbers, then we can divide past 2 again to get ${27}/{250}$. 27 isn't a factor of 250, so the fraction can't be reduced any more. The final reply is ${27}/{250}$. A repeating decimal is 1 that has no end. Since yous can't keep writing or typing the decimal out forever, they are frequently written as a string of digits rounded off (.666666667) or with a bar above the repeating digit(s) $\ov {(.6)}$. For our example, we'll convert .6667 to a fraction. The decimal .6667 is equal to $\ov {(.6)}$, .666666667, .667, etc. They're all but unlike means to show that the decimal is really a string of six'southward that goes on forever. Allow x equal the repeating decimal you're trying to catechumen, and identify the repeating digit(southward). So ten=.6667 vi is the repeating digit, and the stop of the decimal has been rounded up. Multiply by any value of 10 you need to get the repeating digit(due south) on the left side of the decimal. For .6667, we know that six is the repeating digit. We desire that six on the left side of the decimal, which means moving the decimal identify over 1 spot. So we multiply both sides of the equation by (10 x i) or 10. 10x = six.667 Note: You just want ane "prepare" of repeating digit(south) on the left side of the decimal. In this example, with vi as the repeating digit, you lot only want ane vi on the left of the decimal. If the decimal was 0.58585858, yous'd only want one set of "58" on the left side. If it helps, you can motion-picture show all repeating decimals with the infinity bar over them, so .6667 would be$\ov {(.6)}$. Next we want to get an equation where the repeating digit is just to the correct of the decimal. Looking at x = .6667, we can see that the repeating digit (6) is already just to the right of the decimal, so we don't need to do any multiplication. We'll go on this equation as x = .6667 Now we need to solve for x using our two equations, x = .667 and 10x = 6.667. 10x - x =6.667-.667 9x = 6 x = ${6}/{9}$ 10 = ⅔ Convert one.0363636 to a fraction. This question is a bit trickier, simply we'll be doing the same steps that we did to a higher place. Kickoff, make the decimal equal to x, and decide the repeating digit(south). x = i.0363636 and the repeating digits are 3 and half dozen Next, get the repeating digits on the left side of the decimal (again, you just want one set of repeating digits on the left). This involves moving the decimal three places to the right, so both sides need to exist multiplied by (10 x 3) or chiliad. 1000x = 1036.363636 Now get the repeating digits to the right of the decimal. Looking at the equation ten = one.0363636, yous can run across that there currently is a goose egg between the decimal and the repeating digits. The decimal needs to be moved over i space, then both sides need to be multiplied by 10 x i. 10x = 10.363636 Now use the two equations, 1000x = 1036.363636 and 10x = 10.363636, to solve for x. 1000x - 10x = 1036.363636 - 10.363636 990x = 1026 ten = ${1026}/{990}$ Since the numerator is larger than the denominator, this is known as an irregular fraction. Sometimes you can leave the fraction as an irregular fraction, or you may be asked to convert information technology to a regular fraction. Yous tin can do this by subtracting 990/990 from the fraction and making it a 1 that'll get next to the fraction. ${1026}/{990}$ - ${990}/{990}$ = i ${36}/{990}$ x = 1 ${36}/{990}$ ${36}/{990}$ can be simplified by dividing it past 18. 10 = 1 ${two}/{55}$ The easiest fashion to convert a fraction to a decimal is but to use your figurer. The line between the numerator and denominator acts every bit a division line, so ${7}/{29}$ equals vii divided by 29 or .241. If you don't have admission to a calculator though, you tin still catechumen fractions to decimals by using long partition or getting the denominator to equal a multiple of 10. Nosotros explain both these methods in this section. Convert ${3}/{eight}$ to a decimal. Hither is what ${3}/{viii}$ looks similar worked out with long partition. ⅜ converted to a decimal is .375 Convert ${three}/{8}$ to a decimal. We want the denominator, in this example 8, to equal a value of x. Nosotros tin can do this by multiplying the fraction past 125, giving us ${375}/{thou}$. Next we want to become the denominator to equal 1 so we can get rid of the fraction. We'll do this by dividing each part of the fraction by 1000, which means moving the decimal over three places to the left. This gives us ${.375}/{1}$ or just .375, which is our answer. Note that this method only works for a fraction with a denominator that tin easily be multiplied to be a value of x. All the same, there is a trick you can use to judge the value of fractions you lot can't convert using this method. Check out the case beneath. Convert ⅔ to a decimal. There is no number you can multiply 3 by to make it an verbal multiple of 10, only you tin can go close. By multiplying ⅔ by ${333}/{333}$, we get ${666}/{999}$. 999 is very shut to 1000, and so let's act similar it actually is 1000, divide each function of the fraction past 1000, and movement the decimal place of 666 three places to the left, giving us .666 The exact decimal conversion of ⅔ is the repeating decimal .6666667, just .666 gets us very close. So whenever you accept a fraction whose denominator tin't easily be multiplied to a value of ten (this volition happen to all fractions that convert to repeating decimals), just get the denominator every bit close to a multiple of 10 as possible for a close approximate. Below is a chart with common decimal to fraction conversions. You don't demand to memorize these, only knowing at least some of them off the top of your head will brand information technology easy to practice some common conversions. If you're trying to convert a decimal or fraction and don't have a calculator, you can besides run across which value in this chart the number is closest to so y'all can make an educated estimate of the conversion. Decimal Fraction 0.03125 ${one}/{32}$ 0.0625 ${1}/{16}$ 0.1 ${1}/{ten}$ 0.1111 ${1}/{nine}$ 0.125 ${1}/{8}$ 0.16667 ${1}/{6}$ 0.2 ${1}/{5}$ 0.2222 ${2}/{9}$ 0.25 ${1}/{4}$ 0.3 ${3}/{10}$ 0.3333 ${1}/{3}$ 0.375 ${3}/{8}$ 0.iv ${2}/{five}$ 0.4444 ${4}/{9}$ 0.5 ${1}/{two}$ 0.5555 ${5}/{9}$ 0.vi ${iii}/{5}$ 0.625 ${v}/{8}$ 0.6666 ${two}/{3}$ 0.7 ${7}/{10}$ 0.75 ${3}/{4}$ 0.7777 ${7}/{nine}$ 0.8 ${4}/{5}$ 0.8333 ${5}/{half-dozen}$ 0.875 ${7}/{8}$ 0.8888 ${8}/{9}$ 0.9 ${9}/{ten}$ If yous're trying to convert a decimal to fraction, showtime you need to determine if it's a terminal decimal (1 with an end) or a repeating decimal (one with a digit or digit that repeats to infinity). In one case you've done that, y'all can follow a few steps for the decimal to fraction conversion and for writing decimals as fractions. If you're trying to convert a fraction to decimal, the easiest manner is just to use your reckoner. If you don't have 1 handy, you can utilise long sectionalization or become the denominator equal to a multiple of ten, then motion the decimal identify of the numerator over. For quick estimates of decimal to fraction conversions (or vice versa), you tin look at our chart of mutual conversions and see which is closest to your effigy to get a ballpark idea of its conversion value. Want to know the fastest and easiest ways to convert betwixt Fahrenheit and Celsius? We've got y'all covered! Check out our guide to the all-time ways to convert Celsius to Fahrenheit (or vice versa). Are yous learning virtually logarithms and natural logs in math course?We have a guide on all the natural log rules you need to know. Did y'all know that water has a very special density? Bank check out our guide to learn what the density of water is and how the density can change. Need more help with this topic? Bank check out Tutorbase! Our vetted tutor database includes a range of experienced educators who can help you polish an essay for English or explain how derivatives work for Calculus. Yous tin use dozens of filters and search criteria to find the perfect person for your needs. 
How to Catechumen Decimals to Fractions
Converting a Terminating Decimal to a Fraction
Stride 1
Step 2
Step three
Example

Converting a Repeating Decimal to a Fraction
Step 1
Step two
Step 3
Step 4
Example
How to Catechumen Fractions to Decimals
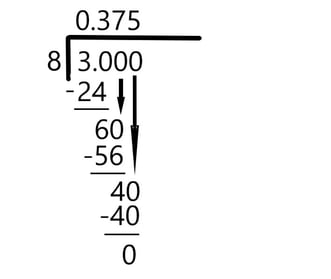
Long Segmentation Method
Denominator equally a Value of 10 Method
Step 1
Step 2
Instance
Common Decimal to Fraction Conversions
Summary: How to Brand a Decimal Into a Fraction
What's Next?


Most the Writer
Christine graduated from Michigan State Academy with degrees in Environmental Biology and Geography and received her Master's from Duke University. In high schoolhouse she scored in the 99th percentile on the SAT and was named a National Merit Finalist. She has taught English and biology in several countries.
25 99 As A Decimal,
Source: https://blog.prepscholar.com/convert-decimal-to-fraction
Posted by: jonesbeink1945.blogspot.com


0 Response to "25 99 As A Decimal"
Post a Comment